어떤 사람이 토끼 1쌍을 우리에 넣었다. 이 토끼 1쌍은 한 달에 새로운 토끼 1쌍을 낳고, 낳은 토끼들도 1달이 지나면 다시 1쌍의 토끼를 낳는다. 그렇다면 1년이 지나면 몇 쌍의 토끼가 있을까?
이 물음에 대한 답을 수열로 나타낸 것을 피보나치 수열이라 한다.
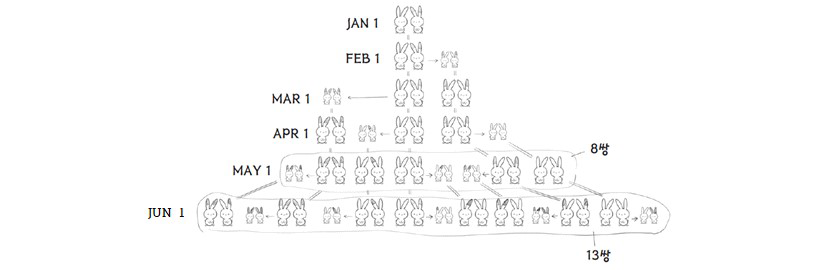

피보나치 수열이 수학적으로 중요한 이유는 수열의 인접한 두 항이 자연에서 자주 발견되는 황금비를 만들기 때문이다. 황금비에 관한 설명은 아래 참고자료에 정리되어 있다.
프로그래밍에서는 피보나치 수열을 구하는 알고리즘이 재귀 함수를 이해하는데 적합해서 팩토리얼과 함께 자주 등장하기 때문에 피보나치 수열을 구하는 방법을 정리해보기로 했다.
피보나치 수열은 이전에 나온 두 값을 합해서 새로운 값이 나오기 때문에 F(n) = F(n-1) + F(n-2)로 나타낼 수 있다. 이에 따라서 수열의 첫 번째와 두 번째 값만 초기값으로 주어진다면 간단하게 n 번째 피보나치 수를 구할 수 있다.
function fibo(n) {
if (n < 2) return n;
return fibo(n - 1) + fibo(n - 2);
}
가장 기본적 풀이인 재귀함수를 이용한 방법이지만 이 방법에는 문제가 있다.
예를 들어 7 번째 피보나치 수를 구한다고 해보자. F(7) = F(6) + F(5)로 나타낼 수 있으므로 F(6)과 F(5)를 구하기 위해 함수를 두 번 호출한다. F(6) = F(5) + F(4), F(5) = F(4) + F(5) 여기까지 오면 함수를 4번 호출하는데 F(5) , F(4)가 반복해서 계산되고 있는 것을 알 수 있다. 구하려는 피보나치 수가 크면 클수록 계산 횟수는 기하급수적으로 늘어난다.
반복 계산을 완벽하게 해결하기 위해서 동적 프로그래밍을 이용하면
function fibo(n) {
let memo = [0, 1];
function recur(n) {
if (memo[n] !== undefined) return memo[n];
memo[n] = recur(n - 1) + recur(n - 2);
return memo[n];
}
return recur(n);
}
배열에 미리 초기값을 주고 한 번 계산한 값은 저장해뒀다가 꺼내 쓰는 방식이기 때문에 반복되는 계산을 피할 수 있다. 만약 재귀함수를 사용하지 않고 반복문을 사용하면
function fibo(n) {
let memo = [0, 1];
for (let i = 2; i <= n; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
return memo[n];
}
재귀와는 다르게 아래 단계부터 n까지 올라가는 방식으로 피보나치 수를 계산할 수 있다.
나만의 풀이
내가 피보나치 수열을 처음 봤을 때 비효율성을 해결하기 위해서 생각했던 방법은 피보나치 수를 계산하는 단계를 건너뛰는 것이었다.
7 번째 피보나치 수를 구한다고 했을 때 F(7)은 다음과 같이 두 개의 피보나치 함수로 표현되면서 단계를 낮출 수 있다.
F(7) = F(6) + F(5) 여기서 F(6)을 F(5)와 F(4)로 쪼개면
F(7) = 2F(5) + F(4)로 나타낼 수 있다.
이를 반복하면
F(7) = F(6) + F(5) = 2F(5) + F(4) = 3F(4) + 2F(3) = 5F(3) + 3F(2) = 8F(2) + 5F(1)
로 나타낼 수 있고 여기서 F앞에 곱해지는 숫자 또한 피보나치 수로 나타낼 수 있는데
한 단계에서 두 단계로 내려가면
F(n) = 2F(n-2) + F(n-3) = F(3)F(n-2) + F(2)F(n-3)
세 단계
F(n) = 3F(n-3) + 2F(n-4) = F(4)F(n-3) + F(3)F(n-4)
규칙성을 보이기 때문에 이를 이용해서 초기값 케이스를 추가시켜 줄수록 더 많은 단계를 건너뛰는 피보나치 함수를 작성할 수 있다.
function fibo(n) {
if (n <= 1) return n;
if (n === 2) return 1;
if (n === 3) return 2; // n 3까지 지정
if (n === 4) return 3; // n 4까지 지정
if (n === 5) return 5; // n 5까지 지정
return 2 * fibo(n - 2) + 1 * fibo(n - 3)
return 3 * fibo(n - 3) + 2 * fibo(n - 4) // n 3까지 지정
return 5 * fibo(n - 4) + 3 * fibo(n - 5) // n 4까지 지정
return 8 * fibo(n - 5) + 5 * fibo(n - 6) // n 5까지 지정
}
처음에 제시한 풀이보다 단계를 건너뛰는 대신 초기값 케이스를 늘려야 하고 단계만 건너뛸 뿐 반복 계산은 여전히 존재한다는 단점이 있다. 그래서 위의 반복문을 사용해서 원하는 단계에 따라 초기값 케이스를 입력해주고 계산하는 방법으로 바꿔보았다.
function fibo(n, steps=2) {
let memo = [0, 1];
for (let i = 2; i <= steps+1; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
function recur(n) {
if (memo[n] !== undefined) return memo[n];
memo[n] = memo[steps+1] * recur(n-steps) + memo[steps] * recur(n-steps-1);
return memo[n];
}
return recur(n);
}
인자로 원하는 피보나치 수 n과 건너뛰는 단계도 받는다.
건너뛰는 단계에 따라 초기값과 리턴 값을 수정해주고 확인해보니


여기서 문제를 발견했다. 처음에 생각할 땐 단계를 건너뛰기 때문에 의미 있는 empty가 많이 발생할 줄 알았지만 계산 과정에서 처음엔 2개의 피보나치 수를 계산하던 것이 점점 늘어나서 steps에 도달하는 순간 empty는 사라지게 된다. 그래서 steps가 얼마일 때 가장 많은 empty를 가지는지 살펴보니 steps가 (n / 3)에 내림한 값을 가졌을 때 가장 많은 empty가 발생한다는 걸 알게 되었다.
function fibo(n) {
let memo = [0, 1, 1];
let steps = Math.floor(n/3);
for (let i = 3; i <= steps+1; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
function recur(n) {
if (memo[n] !== undefined) return memo[n];
memo[n] = memo[steps+1] * recur(n-steps) + memo[steps] * recur(n-steps-1);
return memo[n];
}
return recur(n);
}
이렇게 작성하면 내부함수인 recur함수는 3~4번 호출되고 for문 안의 초기값 설정하는 부분은 (n / 3)만큼 실행된다.

n이 커질수록 더 많은 비율의 empty가 발생해서 fibo(100) 일 때는 63개의 계산을 줄일 수 있다.
사실 피보나치 수의 일반항이 존재하기 때문에 이 방법이 시간 복잡도를 줄이는 데는 의미가 없다. 하지만 이렇게 더 나은 방법을 찾기 위해 고민하고 시행착오를 겪으며 해결해나가는 과정은 의미있지 않을까
참고자료
위키백과, 피보나치 수
삼성디스플레이, 자연과 디자인에서 찾을 수 있는 ‘피보나치 수열’에 숨은 황금비!
Naver, 세상에서 가장 아름다운 비율, 황금비율
Naver, 왜 자연은 피보나치 수열과 황금비를 택했을까
Tistory, 피보나치 수열( 재귀, 동적 프로그래밍, 반복) 모든 방식 알고리즘
Github, 피보나치 수열 알고리즘을 해결하는 5가지 방법
'문제해결 및 일기장' 카테고리의 다른 글
| 코드스테이츠 2주 프로젝트 회고 (0) | 2021.11.23 |
|---|---|
| TIL Amazon Web Service (0) | 2021.11.01 |
| [JavaScript] 프로그래머스 level 1 완주하지 못한 선수 (3) | 2021.08.22 |
| 코드스테이츠 Section 1 후기 (0) | 2021.08.20 |
| 윈도우/Ubuntu 20.04 멀티부팅시 검은 화면이 지속되는 문제 해결법 (0) | 2021.07.20 |